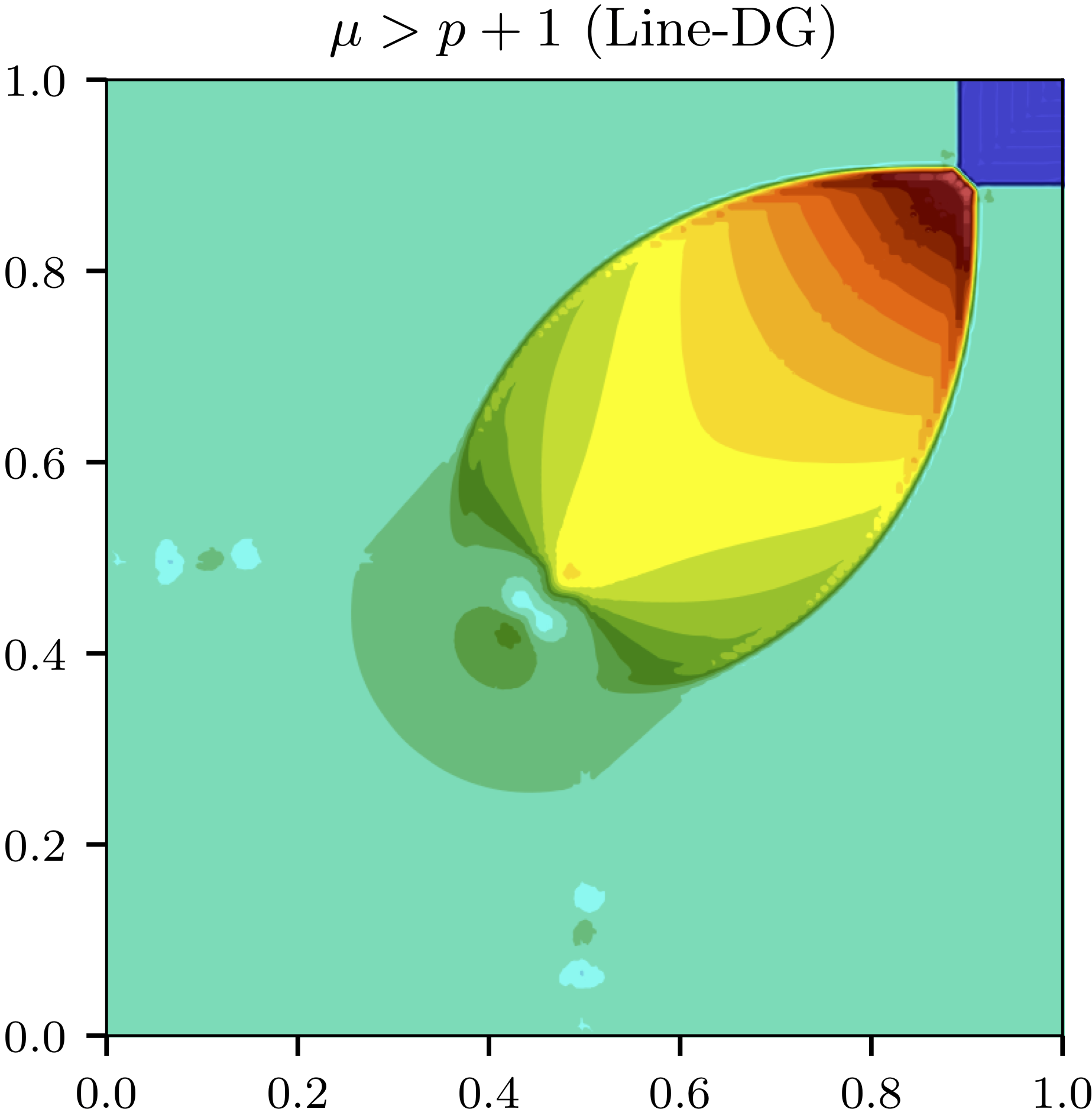
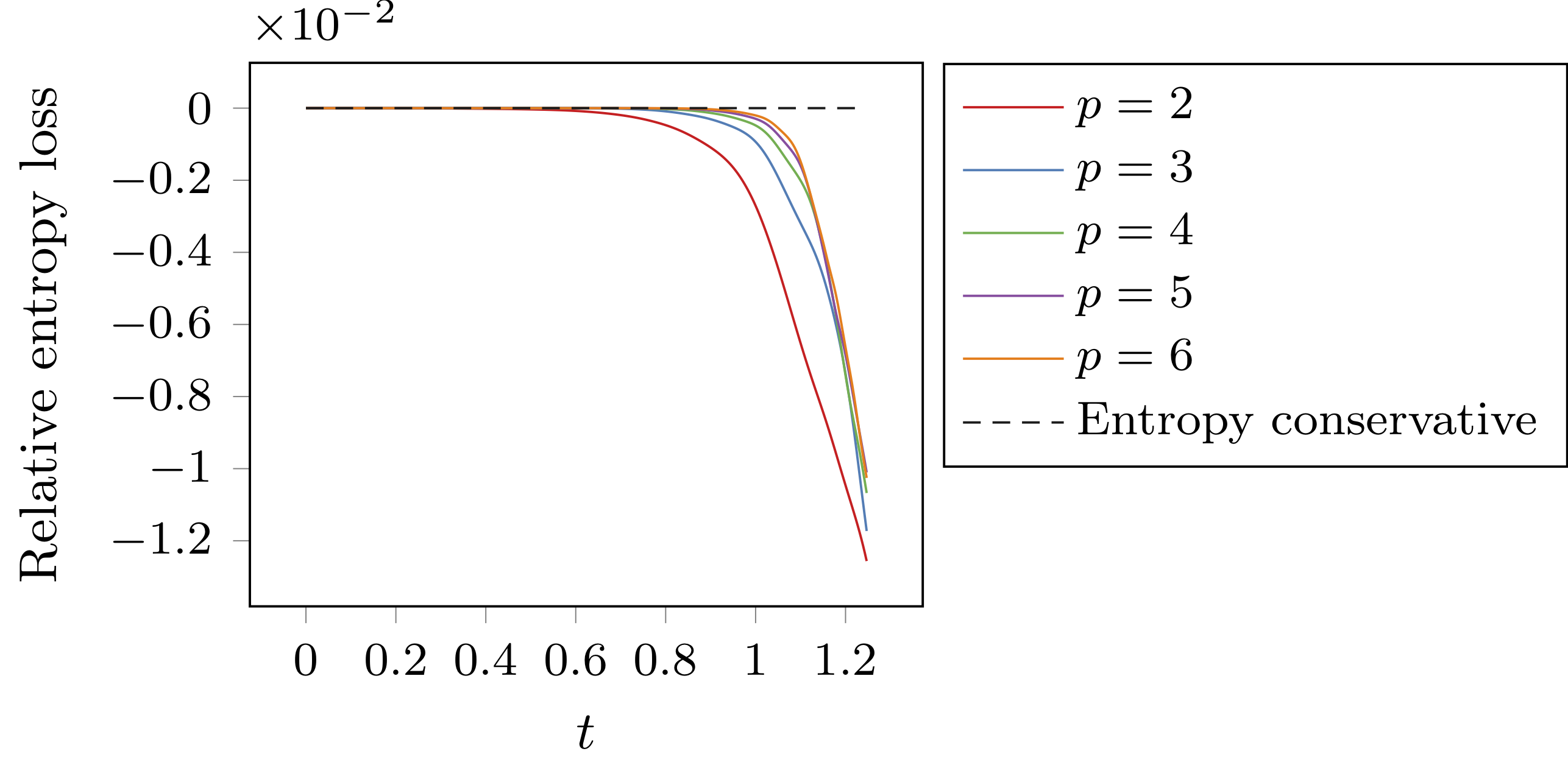
Entropy-stable line-based sparse discretizations
Solutions to hyperbolic conservation laws are known to satisfy an entropy inequality. It is desirable for numerical solutions to these equations to satisfy a discrete analogue of this inequality. This concept, known as entropy stability, is a form of nonlinear stability, which leads to increased robustness and improved results. In our paper we analysed the sparse line-DG method and introduced a modification of this method that leads to discrete entropy stability.
Pictured: Riemann problem for Euler equations (left), and entropy stability and conservation properties (right).
Kronecker-product preconditioners for extremely high-order DG methods
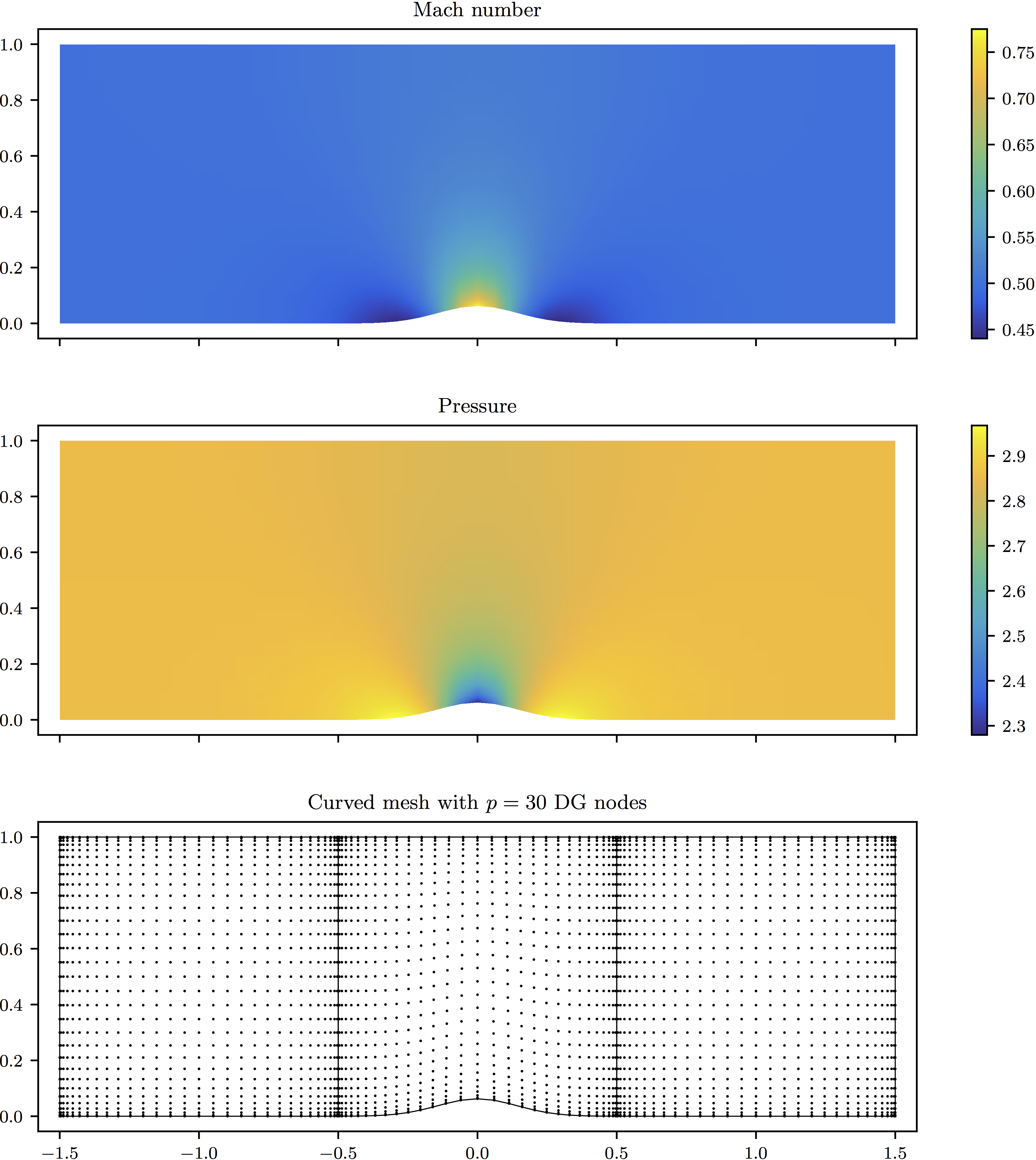
We developed a new class of tensor-product preconditioners that take advantage of sum-factorization techniques to greatly reduce the computational complexity associated with implicit solvers for very high-order DG methods. We have applied these methods to several LES and DNS fluid flow problems in 2D and 3D. Our recent paper was awarded first-place in the 2017 AIAA CFD student paper competition.
More details on the efficient algorithms and numerical results are available in our 2018 JCP paper. These methods have also been extended to second-order system of equations using an interior penalty formulation.
Pictured: Taylor-Green vortex (left), and degree-30 inviscid flow over a bump (right).

Fully-implicit Runge-Kutta time integration for DG
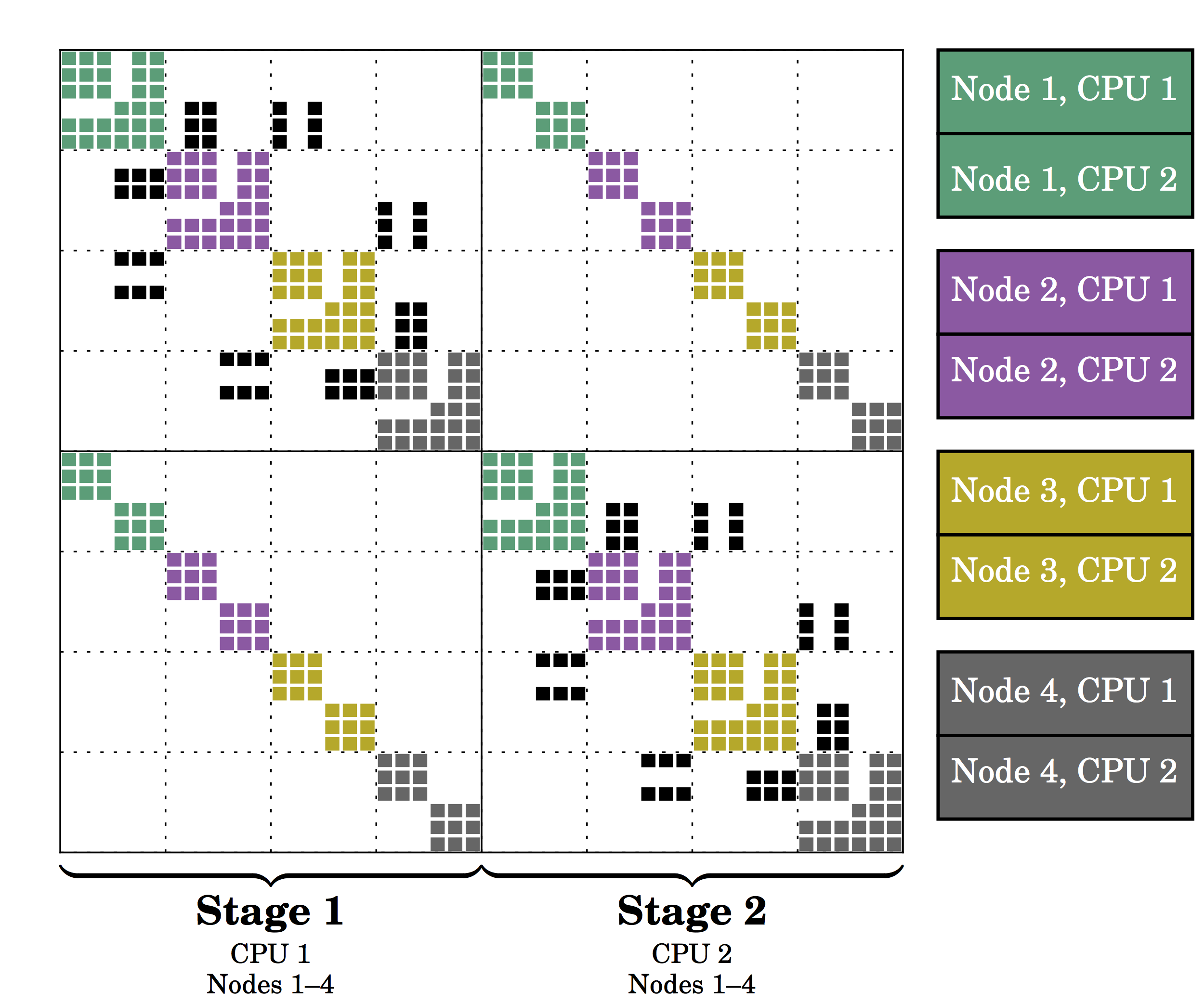
Radau-IIA fully-implicit Runge-Kutta methods have many desirable properties, but the resulting large, coupled systems of equations have been considered prohibitively expensive. We transform the system of equations, to obtain the sparser formulation

which we then precondition using a stage-parallel shifted ILU(0) preconditioner. Details are available in our 2017 JCP paper.
These fully-implicit solvers have also been extended to the adjoint equations for use in PDE-constrained optimization problems. Further applications of this method include the study of transonic buffeting at high Reynolds number.
Pictured: Stage-parallel strategy for hybrid shared-distributed memory supercomputers (left), and LES over a NACA in 3D using 3-stage fifth-order IRK.

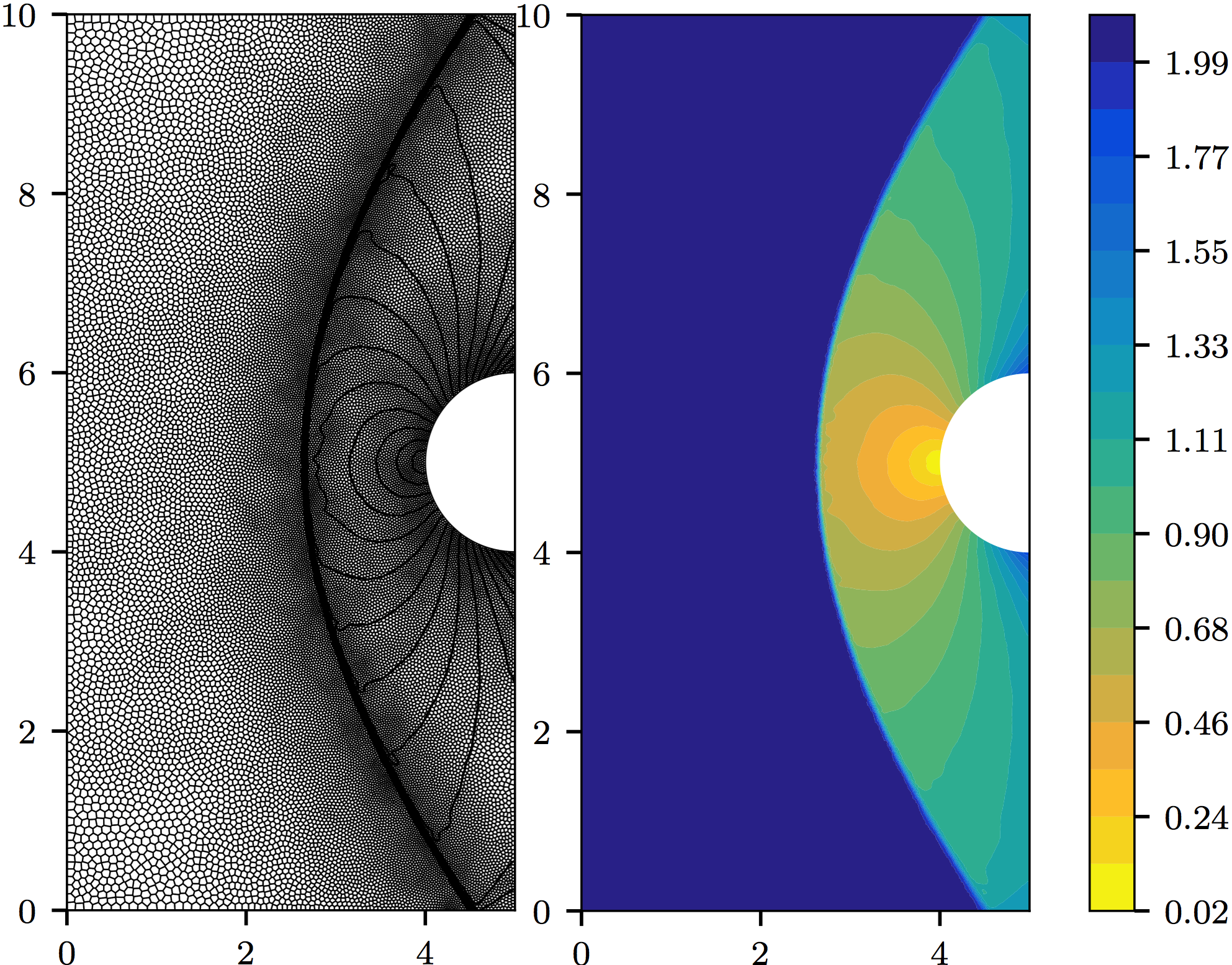
Convergence of iterative solvers for polygonal DG methods
We investigated the convergence of iterative linear solvers (such as block Jacobi or GMRES-ILU(0)) when applied to discontinuous Galerkin methods on arbitrary polygonal meshes. A von Neumann analysis demonstrated that polygonal meshes can result in faster iterative convergence, and a series of numerical examples corroborate this result. More details can be found in our CAMCoS paper.
Pictured: a polygonal mesh refined in the vicinity of a supersonic shock.
High-order time integration for low-Mach combustion
This research project, in collaboration with scientists from Center for Computational Science and Engineering at Lawrence Berkeley National Lab, was concerned with the development of high-order time integration schemes for low-Mach number combustion. A new strategy for employing multi-implicit spectral deferred corrections (MISDC) was used in conjunction with a fourth-order finite volume method in order to obtain overall fourth-order convergence for hydrogen, methane, and dimethyl ether flame simulations. The results were published in our 2016 paper.